One-sentence Summary

Researchers from Shanghai Jiao Tong, Tsinghua, NUS, Microsoft, and HKBU propose Qute, a quantum database compiling SQL into efficient circuits, using hybrid optimization and selective indexing to outperform classical systems on real hardware, advancing toward quantum-native data management.

Key Contributions

• Qute introduces a quantum-native database architecture that compiles extended SQL into gate-efficient quantum circuits, enabling quantum computation as a first-class execution substrate rather than a simulation-based accelerator.
• It features a hybrid optimizer that dynamically selects between quantum and classical execution plans and employs selective quantum indexing to handle qubit constraints, while using fidelity-preserving storage to maintain data usability under quantum noise.
• Deployed on the real quantum processor origin_wukong, Qute demonstrates measurable performance gains over classical baselines at scale, validating its practical feasibility and releasing an open-source prototype for community use.

Introduction

The authors leverage quantum computing as a first-class execution substrate within a database system, aiming to accelerate workloads like full-table scans by mapping SQL operators to quantum circuits and using algorithms such as Grover’s search. Prior approaches either simulate quantum execution on classical hardware or treat quantum computation as an isolated accelerator, lacking end-to-end integration and failing to address quantum-specific constraints like noise, qubit limits, and fidelity loss. Qute’s main contribution is a unified architecture that compiles extended SQL into gate-efficient quantum circuits, employs a hybrid optimizer to dynamically choose between quantum and classical execution, introduces selective quantum indexing to reduce qubit usage, and designs fidelity-preserving storage to maintain data usability under current hardware limitations.

Method

The authors leverage a hybrid quantum-classical architecture to enable efficient execution of relational operations on quantum hardware, while preserving correctness and adapting to hardware constraints. The system, Qute, is structured around three core components: a quantum-aware query engine, a storage engine optimized for quantum data formats, and a fidelity-aware optimizer that dynamically selects between quantum and classical execution paths.

The query engine begins with a quantum-aware parser that classifies SQL operators into exact, statistical, or approximate categories. These are then compiled into quantum circuits via a modular operator compiler that generates gate-efficient implementations for filtering, joins, and aggregation. The compiler employs a three-tier intermediate representation—logical, quantum-extended, and physical circuit IR—to progressively lower declarative queries into executable quantum circuits. As shown in the figure below, the query optimizer uses a fidelity-aware cost model that evaluates each quantum operator using a tuple $(T_q, P_q, \varepsilon_q)$(Tq​,Pq​,εq​), capturing latency, success probability, and approximation error. This enables hybrid plan generation, where both quantum and classical implementations of operators are embedded in the execution plan, allowing runtime adaptation based on observed hardware conditions.

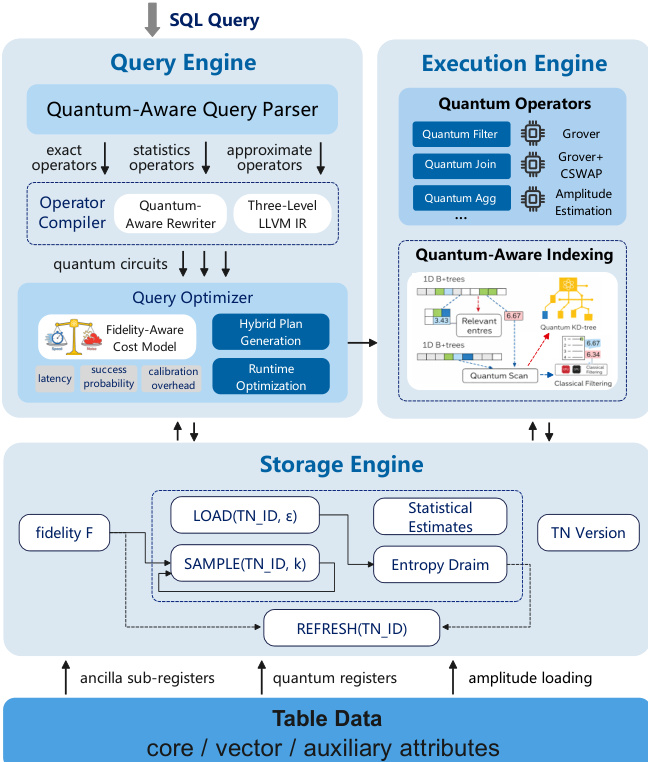
The storage engine adopts a state-centric design, storing quantum-active attributes as compressed tensor networks (TNs) that support bounded reconstruction and sampling under fidelity constraints. Core data is encoded using three schemes: basis encoding for row identifiers, amplitude encoding for numerical vectors, and control encoding for metadata flags stored in ancilla qubits. The engine exposes fidelity-aware primitives such as LOAD(TN_ID, ϵ), SAMPLE(TN_ID, k), and REFRESH(TN_ID) to manage entropy and noise during access. Classical metadata is maintained separately to ensure recoverability.

For quantum-accelerated operators, Qute reformulates classical database primitives into quantum circuits that exploit amplitude-level parallelism. For filtering, it adapts Grover’s algorithm: row identifiers are mapped to a search space, and predicates are compiled into an oracle $O_\phi$Oϕ​ that marks satisfying rows via phase inversion. Compound predicates are implemented using ancilla-assisted multi-controlled gates. After Grover iterations amplify the amplitudes of matching rows, classical reconciliation ensures correctness by deduplicating and revalidating results.

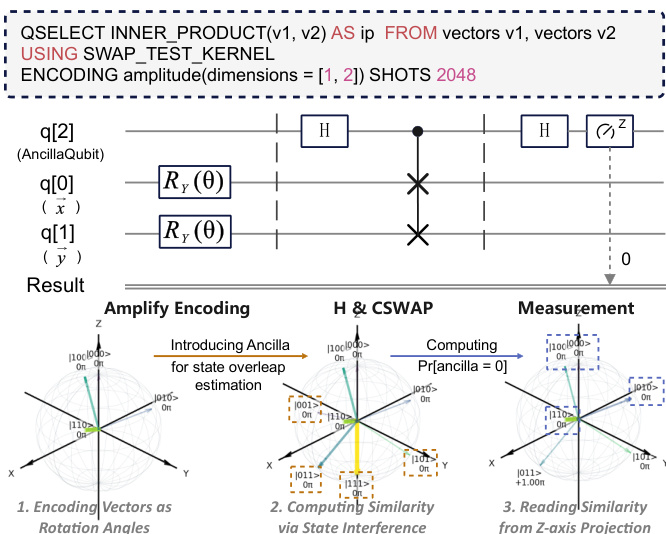
For similarity joins, Qute encodes vectors into quantum states using parameterized $R_Y(\theta)$RY​(θ) rotations and estimates their inner product via the SWAP test. As illustrated in the figure below, an ancilla qubit is initialized into superposition, a CSWAP gate is applied conditionally between the two data registers, and a final Hadamard gate enables measurement of the overlap probability. The inner product is estimated as $|\langle x|y\rangle|^2 = 2 \cdot \text{Pr}[\text{ancilla} = 0] - 1$∣⟨x∣y⟩∣2=2⋅Pr[ancilla=0]−1, enabling efficient similarity detection without explicit dimension-wise traversal.

Aggregation is reformulated as a probability estimation task. A uniform superposition over all row identifiers is prepared, and each row’s value $v(x)$v(x) controls a “Good” qubit via a rotation whose angle is proportional to $v(x)/V_{\max}$v(x)/Vmax​. The probability of measuring the Good qubit as $|1\rangle$∣1⟩ corresponds to the normalized average value, from which the global sum is recovered via amplitude estimation: $\text{SUM}(v) = N \cdot V_{\max} \cdot \text{Pr}[\text{Good} = 1]$SUM(v)=N⋅Vmax​⋅Pr[Good=1].

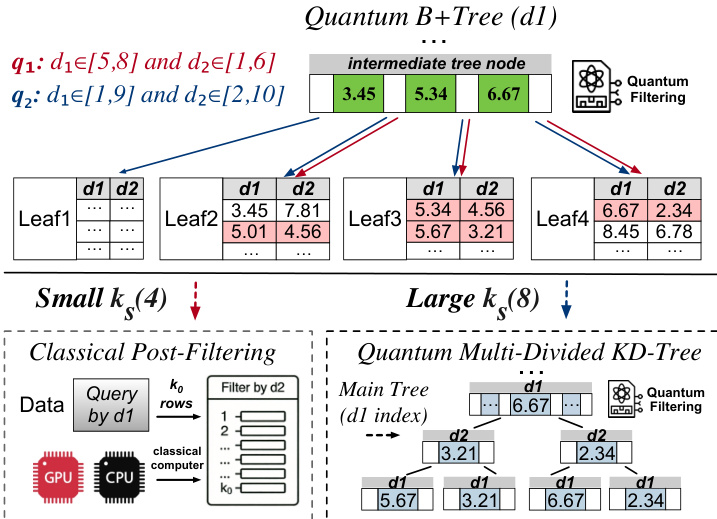
To mitigate quantum memory constraints, Qute employs quantum-aware indexing. For multi-dimensional queries, it first probes lightweight quantum B⁺-trees on individual dimensions to identify candidate sets. If the candidate size $k_s$ks​ is small (e.g., $O(\log N)$O(logN)), classical post-filtering is applied. If $k_s$ks​ is large, the system escalates to a quantum multi-divided KD-tree that jointly indexes multiple dimensions, recursively pruning the search space using quantum-assisted probing. As shown in the figure below, this hybrid strategy dynamically selects between classical and quantum paths based on the cardinality of intermediate results.

The optimizer models quantum operators as stochastic, accuracy-bounded primitives. Time estimation $T_q$Tq​ accounts for gate durations and control overheads across circuit layers. Success probability $P_q$Pq​ is derived from gate error rates and decoherence, approximated as $P_q = \prod_{k=1}^{K} p_k$Pq​=∏k=1K​pk​, where $p_k = (1 - \sum_{g \in L_k} \epsilon_g) \cdot \exp(-t_k / T_2^{\text{eff}})$pk​=(1−∑g∈Lk​​ϵg​)⋅exp(−tk​/T2eff​). Hybrid execution error $\varepsilon_q$εq​ is incorporated via a fallback model: $\mathbb{E}[T_q] = P_q \cdot T_q^{\text{quantum}} + (1 - P_q) \cdot T_q^{\text{classical}}$E[Tq​]=Pq​⋅Tqquantum​+(1−Pq​)⋅Tqclassical​. Runtime optimization adapts to noise by increasing shots, switching circuit variants, or falling back to classical execution—all under bounded-error semantics to ensure result trustworthiness.

Experiment

• Implemented a minimal Qute prototype offloading data filtering to a 72-qubit noisy QPU, using QPanda3 and origin_wukong, with 2000 shots per experiment.
• Evaluated on a synthetic dataset of 2^40 tuples using selective filter queries, with predicate selectivity capped at 2%.
• Compared Qute against a classical database using a cost-model-based approach to ensure fair algorithmic comparison.
• Measured and modeled Qute performance showed strong agreement, validating the cost model for large-scale extrapolation.
• Qute underperforms classical systems on small datasets but surpasses them beyond ~2^30 tuples, demonstrating scalability for extreme-scale unindexed filtering.