一句话总结

来自谷歌及合作者的研究人员提出使用 Gemini 评估 Bloom 的 Erdős 问题数据库中的 700 个开放数学猜想，通过新颖的 AI 解法或重新发现的文献解决了其中 13 个问题，揭示“开放”状态往往反映的是问题的冷门程度而非难度，同时警示 AI 在大规模数学发现中存在无意识抄袭的风险。

主要贡献

• 我们应用 Gemini，采用人机混合工作流评估了 Bloom 的 Erdős 问题数据库中的 700 个“开放”猜想，先通过自然语言验证缩小范围，再经专家验证，最终解决了 13 个问题——其中 5 个由 AI 自主提出新解，8 个通过重新发现已有文献解决。
• 我们的结果表明，这些问题的“开放”状态往往源于其冷门性而非内在难度，因为 AI 高效挖掘出被忽视或已被平凡解决的猜想，挑战了数据库中关于问题难度的既有假设。
• 我们记录了 AI 在数学发现规模化应用中的关键挑战，包括全面文献检索的困难，以及 AI 无意中复现已知结果而未加引用的风险，我们称之为“无意识抄袭”。

引言

作者利用 Gemini 评估 Bloom 的 Erdős 问题数据库中的 700 个“开放”猜想，借助 AI 驱动的自然语言验证在人工专家审查前筛选候选问题。这一方法至关重要，因为它扩展了 AI 辅助数学发现的规模——专家评估受限于时间和人力稀缺。先前研究在大规模验证正确性及识别文献中是否已有解方面面临挑战，常导致重复或误导性结论。作者的主要贡献是解决了 13 个问题：5 个看似新颖的自主解，8 个通过发现已有文献解决，揭示许多“开放”问题其实只是冷门而非困难。他们还强调了系统性问题，如 AI 存在无意识抄袭风险及文献检索困难——这些问题无法通过形式化验证解决。

方法

作者利用几何关联框架，建立 $\alpha_k$αk​ 增长率的下界，其中 $\alpha_k$αk​ 定义为平面上 $n$n 个点集中任意一点所确定的不同距离的最小数量。该方法的核心是构造一组由精心选择的 $k$k 个点导出的圆族，再应用已知的关联界，推导出除非 $\alpha_k$αk​ 至少以 $k^{1/4}$k1/4 的速度增长，否则将导致矛盾。

构造从选取点集 $P_n = \{x_1, \ldots, x_n\} \subset \mathbb{R}^2$Pn​={x1​,…,xn​}⊂R2 开始，按 $R(x_i)$R(xi​)（即 $x_i$xi​ 到 $P_n$Pn​ 中其余点的不同距离数）非递减排序。前 $k$k 个点 $S = \{x_1, \ldots, x_k\}$S={x1​,…,xk​} 用于定义圆族 $\mathcal{C} = \bigcup_{i=1}^{k} \{ \Gamma(x_i, r) : r \in D_i \}$C=⋃i=1k​{Γ(xi​,r):r∈Di​}，其中 $D_i$Di​ 是 $x_i$xi​ 到 $P_n$Pn​ 其余点的不同距离集合。由于每个 $|D_i| < \alpha_k n^{1/2}$∣Di​∣<αk​n1/2，圆的总数满足 $|\mathcal{C}| < k \alpha_k n^{1/2}$∣C∣<kαk​n1/2。

关键洞见在于，每个点 $p \in P_n \setminus S$p∈Pn​∖S 至少位于 $\mathcal{C}$C 中 $k$k 个圆上（每个中心在 $S$S 中各对应一个）。这给出了 $P_n$Pn​ 与 $\mathcal{C}$C 之间关联数的下界：$(n - k)k$(n−k)k。应用 Pach–Sharir 关联界（定理 1），取 $k=3$k=3、$s=2$s=2（针对圆），关联数上界为 $c(3,2) \left( n^{3/5} |\mathcal{C}|^{4/5} + n + |\mathcal{C}| \right)$c(3,2)(n3/5∣C∣4/5+n+∣C∣)。代入 $|\mathcal{C}|$∣C∣ 的上界并令 $n \to \infty$n→∞，得 $k \leq C(\alpha_k^{4/5} k^{4/5} + 1)$k≤C(αk4/5​k4/5+1)，从而推出 $\alpha_k = \Omega(k^{1/4})$αk​=Ω(k1/4)。

该方法依赖几何构造与组合关联界的交互，将距离分布问题转化为曲线-点关联问题，再通过渐近分析提取所需增长率。

实验

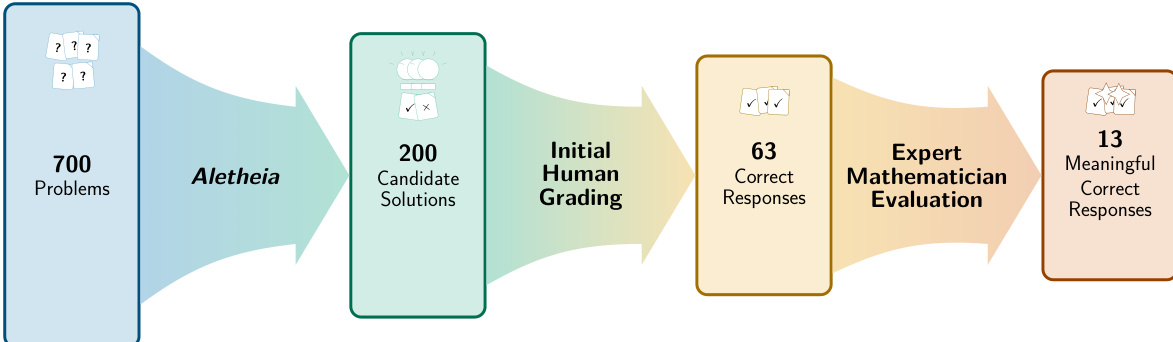
• 基于 Gemini Deep Think 构建的数学研究代理 Aletheia 评估了 700 个开放的 Erdős 问题，得出 63 个技术上正确的解，但仅 13 个有意义地回应了 Erdős 的原始问题陈述；50 个正确解因误解而数学上平凡，12 个含糊不清。
• 人工评估显示，200 个评分响应中有 68.5% 存在根本性缺陷，凸显验证 AI 输出的高昂成本，包括调试错误及检查文献重叠或无意抄袭。
• 在 13 个有意义的正确解中，5 个为自主新颖解（Erdős-652, 654, 935, 1040, 1051），但均未达到独立研究论文水平；Erdős-1051 后被扩展为合作论文。
• Aletheia 还识别出 8 个已在文献中解决的问题（如 Erdős-333, 591, 705），并独立重新发现 3 个解（如 Erdős-397, 659, 1089），引发对训练数据中无意识抄袭的担忧。
• 最终验证显示，部分“已解决”问题存在缺陷或表述模糊，如 Erdős-75，其列出的问题实为对 Erdős 原意的误述，凸显 AI 驱动研究中精确问题表述的必要性。
• 本工作强调，尽管 AI 可辅助数学发现，其输出仍需严格的人工审查，所谓“加速科学”的主张必须考虑验证和语境准确性所隐藏的人力成本。

作者使用专用 AI 代理为 700 个开放 Erdős 问题生成解，随后由人类数学家评估 200 个候选响应。结果显示，尽管 31.5% 的响应技术上正确，但仅 6.5% 有意义地回应了预期数学问题，凸显 AI 生成数学中语法正确性与语义相关性之间的差距。评估强调，在评估 AI 对数学研究的贡献时，必须进行严格的人工监督与语境理解。